栈混洗

2020-11-27

考察三个栈A、B、S，其中B、S初始为空。A中含有个元素，
（尖括号为栈顶，方括号表示栈底）若只允许通过弹出栈A的顶元素，随机压入栈S，或通过弹出S的顶元素并压入栈B，则经过这两种操作各次，栈A、S均为空，原A中的元素全部转入B，此时，称此序列为原序列的一个栈混洗。

对于长度为n的输入序列，每一个栈混洗都对应于由栈S的n次push操作和n次pop操作所构成的某一合法操作序列。
例如，对于，即对应于操作序列：

${push,push,push,pop,pop,push,pop,pop}$

反过来，由n次push和n次pop构成的任何操作序列，只要满足任一前缀中的push不少于pop这一条件，则该序列唯一对应于某个栈混洗。

栈混洗的甄别

设B为A = { 1, 2, 3, …, n }的任一排列。
试证明，B是A的一个栈混洗，当且仅当对于任意，B中都不含如下模式：

先证明“仅当”，采用反证法。
注意到，对于输入序列的任意三个元素，其在输出序列中的相对次序，与其他元素无关。因此，只需关注只有三个元素的情况。任何情形下，前面的元素必然先于后面的元素弹出栈A并压入栈S。若输出序列存在，k最先在S中出栈，那么，i,j必已在栈S中，且j在上，i在下。这意味着，该输出次序必然是，而非。

既然以上规律与其余元素无关，{ k, i, j }即可视作判定整体输出序列不可行的一个特征，我们不妨称之为“禁形”(forbidden pattern)

再证明“当”。
按照如下算法，对于不含禁形的输出序列，均可模拟出其栈混洗的过程

void stackPermutation ( stack<T> B, stack<T> A )
{
    stack<T> RB;
    while(!B.empty()) RB.push(B.pop());
    stack<T> S;
    while(!RB.empty())
    {
        while( S.empty() || RB.top()!=S.top() )
        {
            S.push(A.pop());
            //cout<<"push"<<" ";
        }
        S.pop();
        RB.pop();
        //cout<<"pop"<<" ";
    }
}//O(n)

若对任意，B中都不含模式，则B是否必为A的一个栈混洗？

此类禁形是前面禁形的特例，将

分别称作“915”式禁形、“615”式禁形。
只需证明：只要B中含有“915”式禁形，则必然也含有“615”式禁形
做数学归纳。假定对于任何的，以上命题成立，考虑的情况。
不妨设，于是在B中相对于的位置有两种可能：
1）在的左侧
此时，即为“915”式禁形，由归纳假设，必有“615”式禁形
2）在的右侧
此时，即构成一个“615”式禁形。

栈混洗的计数

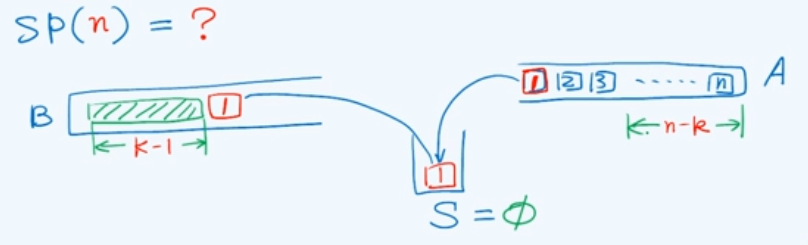
考虑第一个元素是第k个被压入栈B的元素的情形，由于其在S的栈底，此时栈S为空，栈A中留有n-k个元素。
由乘法原理可得共有种情况，
再由加法原理，

$SP(n)=\sum_{k=1}^{n}{SP(k-1) \times SP(n-k)}$

考虑边界情况，
可以解得结果为

$SP(n)=\frac{(2n)!}{(n+1)!\cdot n!}$

即著名的卡特兰数。