Number of trees with n labeled vertices——CayleyTheorem

Combinatorial problem: How many trees can be created with n labeled vertices?

English mathematician Cayley sloved this problem and proposed Cayley Theorem: the number of trees with n labeled vertices is .
To prove the theorem, we need absolutly simplify a tree to a number sequence, for example,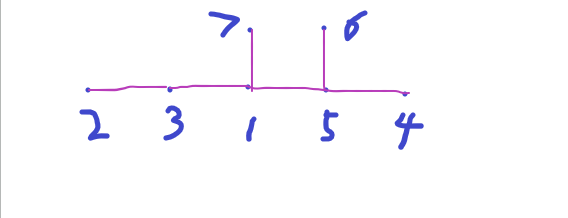

we cut out the smallest one among all the leaf nodes and write down its parent node and go on until only 2 nodes left.
Firstly,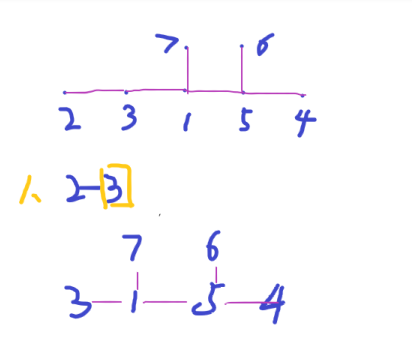

secondly,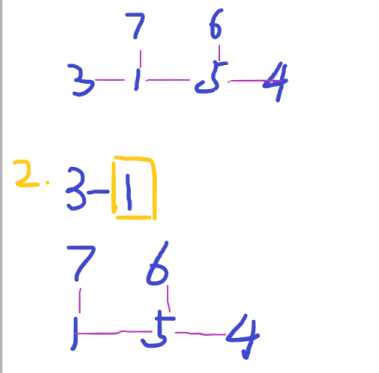

thirdly,

then,

finally,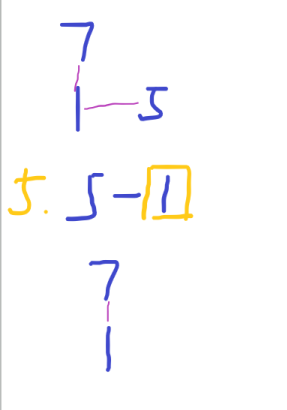

Now we have the sequence,

It is natural to doubt that if it is a necessary and sufficient condition.In other words, whether can a sequence be restored to the unique tree? Of course yes.
It will be completed in several steps:
In the sequence 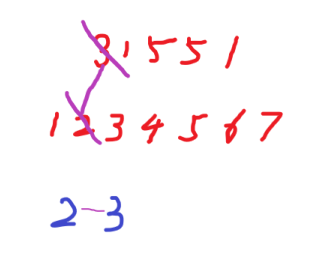, we focus on the first number , and pick out the minimum number in but not appearing in . Obviously it’s . Then eliminate the 2 numbers and link the 2 nodes ralatively, as shown in the figure below,

Repeat this proceedings,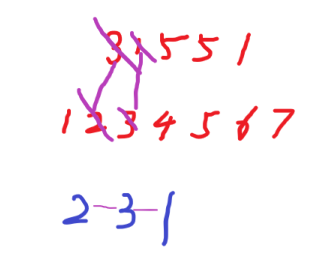




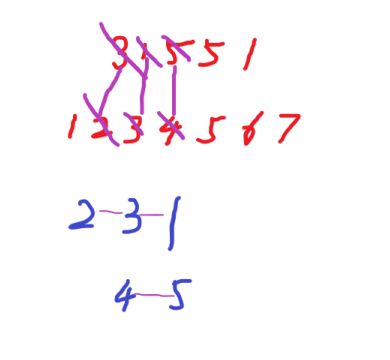
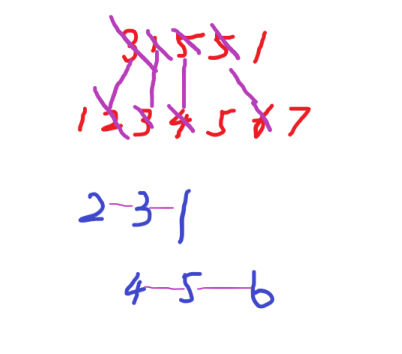
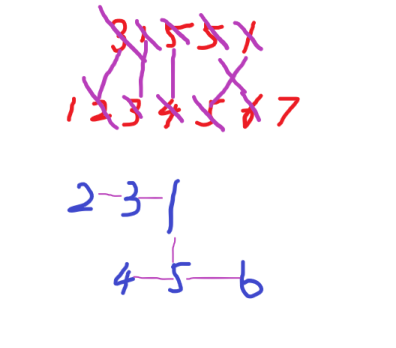
now only number 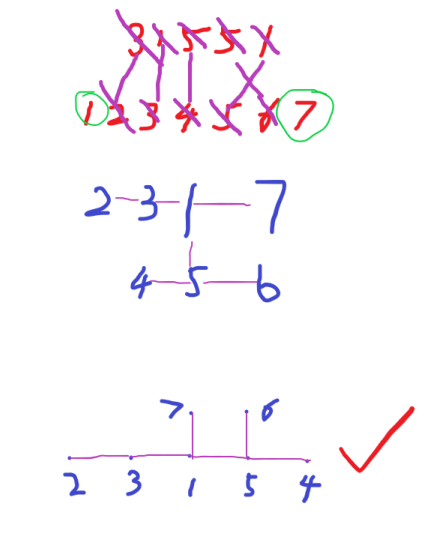and number left, connect them and we get the primary tree,

So we have found that a n-node tree uniquely coresponds to a (n-2)-number sequence. Besides, 2 arbitrary numbers of the sequence can be equal[WHY?].
Hence, each number has n choices and there are n-2 numbers. According to Multiplication Principle, different conditions exist.
Therefore we can say, n labeled vertices create trees.